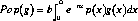
September 16, 1995
Preliminary Draft
Intergenerational Transfers and the Economic Life Cycle: A Cross-Cultural Perspective
Ronald Lee
Demography and Economics
University of California
2232 Piedmont Ave
Berkeley, CA 94720
This paper was prepared for presentation at a seminar on intergenerational transfers, sponsored by the IUSSP and the Population Program of the East West Institute in Hawaii. I am grateful to David Dodds, Carl Mason, Diana Friou, Guy Stecklov, Tim Miller and Antoine Bommier for many helpful discussions and for permission to borrow from the results of their ongoing research. Hillard Kaplan generously made available the tabulated data for the Amazonian groups he has studies. The research on which this paper was based was funded by a grant from NIA, AG11761-01A1.
A Cross-Cultural Perspective on Intergenerational Transfers and the Economic Life Cycle
Abstract
Consumption and labor earnings differ markedly from one another over the life cycle. These differences are made possible by various kinds of reallocations from one age to another. The reallocations take many forms, but they can be grouped into three analytically motivated categories.
Reallocations of resources across age and time take place in many ways and for many reasons. Positive interest rates encourage people to defer consumption. This incentive is reinforced by a bio-cultural-institutional-behavioral need to provide for consumption in old age when productivity falls or retirement occurs, by a desire to leave bequests for children, and by a desire to hedge against future risk. Furthermore, in some settings parents may be able to capture the surplus production of their young children, or their adult children may support them in old age. All these factors tend to make labor earning exceed consumption at younger ages and for consumption to exceed earnings at older ages, which requires a net upward reallocation of income across age, from younger to older. At the same time, however, impatience and uncertainty about survival, as emphasized by Fisher, encourage consumption in advance of earnings. This tendency is reinforced by the costs of rearing children and perhaps by the receipt of bequests. These factors tend to make consumption exceed labor earnings at younger ages, and the reverse at older ages, which requires a downward reallocation of income across age, from older to younger.
We can imagine that each person, even a child, accumulates wealth when consumption is less than earnings, and draws down wealth or goes into debt when consumption exceeds earnings. With suitable discounting, we can then associate a level of wealth with a person at each age. This is called "life cycle wealth"; it is the wealth necessary in order to achieve the desired path of consumption over the life cycle. I will later show that when net reallocations of income are on average upwards in the population, then the average person will hold positive life cycle wealth, and when net reallocations are on average downwards in the population, then the average person will hold negative life cycle wealth. The direction in which income is reallocated in a population and the sign of average life cycle wealth are fundamental features of an economy.
Reallocations take place in many different ways. Some are enforced by law, and flow through the public sector, such as Social Security, Medicare, Medicaid, public education and a host of smaller programs, and their associated taxes. Others reflect individual decisions about fertility, investment in children, bequests, private provision for old age, purchases of houses, cars or lesser durables and so on. In this case, the vehicles range from credit card debt, car loans and mortgages through the stock and bond markets and private pensions and annuities, to stuffing money under the mattress.
In this paper, after developing an analytic framwork for addressing these issues, I attempt to measure the direction of reallocations in societies ranging from hunter/gatherer/horticulturalists of the Amazon Basin, to the contemporary U.S. Where possible, I go beyond examining the direction of these reallocations to say something about the mechanisms and institutions through which the reallocations are achieved. I will show that there are three broad kinds of mechanisms through which resources can be reallocated: 1) the accumulation and decumulation of real wealth, or capital; 2) borrowing and lending, or credit transactions; and 3) outright gifts with no quid pro quo, or transfers. Throughout the paper, the main emphasis will be on transfers, which will be seen to have some special properties which give them a unique role in the macro-economy.
The study of transfers may appear to be an esoteric and narrow topic of little general interest or importance. Before proceeding, therefore, it will be useful to discuss the ways in which transfers matter, and at the same time to briefly introduce some of the literature in this area:
There are many important and influential contributions to the literature on interage transfers, some of which were cited above. Yet the possibilities for systematic integration of work on these topics have not been fully realized, and the time is ripe for synthesis and for progress on some new fronts. The theoretical literature, starting with Samuelson's (1958) seminal article, has mainly analyzed the case of a population with two age groups, in which there is one hundred percent survival until the end of the second age group, at which point all die [1]. The two age group assumption means that one cannot consider the three stages of the human economic life cycle together--childhood, working years, and retirement. This severely limits the problems that can be examined. The rectangular survival assumption means that one cannot consider the effects of declining mortality on the life cycle, nor distinguish between changes in population growth rates originating in fertility or in morality. This is also a severe limitation. Finally, the highly schematic and abstract nature of both assumptions means that there is no possibility at all of implementing the models empirically [2].
More empirical studies typically look in detail at specific transfer systems, but the results are not placed in the framework of the overlapping generations model. While the present paper does not develop much explicit theory, the framework employed has also been used to derive a number of the formal results of the classic overlapping generations literature in a more general demographic context (Bommier and Lee, 1995).
As mentioned earlier, there are many ways in which reallocations take place. Despite this great variety of market and non-market mechanisms, there is a simple, suggestive, and analytically useful way to categorize what I will call these "reallocation systems". By a reallocation system, I mean, loosely speaking, a self-contained collection of flows by age. For example, the Social Security reallocation system includes both the benefits and the related payroll taxes, as does Medicare. Only the portion of payroll taxes needed to offset the benefits and meet administrative costs is part of the Social Security transfer system; that portion of payroll taxes that is in principle used to accumulate a reserve fund is counted as part of some other system--possibly the federal debt system, possibly public sector capital accumulation. Childrearing is a familial transfer system, consisting of the support parents give to their children, and the support children receive from their parents; these constitute a closed system. Similarly, the age profiles of making bequests and receiving bequests together constitute a system. There is no particular level at which disaggregation should stop; different levels are appropriate for different questions. In one context, we might work with a system of government transfers; in another context, we might restrict attention to the federal transfer system; and in another context, we might examine the AFDC transfer system which cuts across federal and state governments. However, the discussion that follows establishes a minimum level of disaggregation that is necessary to achieve analytically appropriate categories.
A net reallocation schedule, g(x), derives from gross schedules, g+(x) and g-(x), describing flows into (+) and out of (-) the household or individual budget of surviving members or the population. For example, g+(x) might be Social Security benefits received, and g-(x) might be payroll taxes. At any age x, the sum of labor earnings plus all net reallocations minus consumption equals zero (where the reallocations must be defined in an exclusive, that is non-redundant, way).
These concepts can be illustrated by the example of the Social Security system in the U.S., which is mainly a public sector pension system. Figure 1 (reproduced from Lee and Miller, 1995) plots the relevant age schedules. Panel A shows g+(x) and g-(x), the gross in and out flows corresponding to benefits received by age and taxes paid by age into the system. The schedule of benefits also includes some payments for disability and for benefits to survivors of the primary insured, in addition to pensions, but pensions dominate the picture. Panel B shows the net reallocation system, g(x), which is just the sum of these two. Panel C shows the transfer wealth generated by the system for the average person at each age, calculated as the survival weighted present value of expected future receipts of benefits from the system minus the expected future payment of taxes, assuming that these age profiles remain fixed in the future. The plotted W(x) schedule assumes that the market rate of interest, r, exceeds the sum of the population growth rate and the growth rate of the productivity of labor by .04--probably an unrealistically high amount.
Much of the discussion which follows does not need to assume a stable population or an economic steady state (see Bommier and Lee, 1995, for example), but for the most part I will make these assumptions here in order to simplify the exposition. Thus I will assume that the age profiles of reallocation systems are fixed over time, which is of course unrealistic. In most cases neither the analytic framework nor the empirical results are altered if it is instead assumed that the cross-sectional shape of the reallocation profile remains fixed while the level shifts upward at a constant rate equal to the growth rate of labor productivity. However, in many cases this kind of assumption will be violated: pensions systems may be extended to cover an increasing share of the population, housing prices and the value of housing services may rise much more rapidly than the general price level, and in general the problem of capital gains and losses may be significant, to mention only a few of the many difficulties. In principle, the analysis can also be carried out on changing age schedules for reallocation systems, as is done, for example, in empirical implementations of generational accounting (see Auerbach et al, 1991).
For any system of reallocation g, the gross flow schedules g+ and g- can each have any shape, sign and magnitude. However, their sum, the net allocation schedule g = g+ + g-, may be subject to certain constraints. Suppose we weight a schedule g by the stable age distribution, and sum over all ages; call this operation Pop(g):
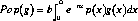
where b is the crude birth rate and n the growth rate in the stable population, and p(x) is the survival schedule. For any reallocation schedule g, this sum either equals zero or does not equal zero. Alternatively, suppose we calculate the survival-weighted present value of g at birth discounted at rate r; call this operation PV(g).
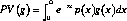
PV(g) also either equals zero or it does not.
We can define a four way classification of reallocation systems g, depending on whether or not Pop(g)=0, and whether or not PV(g)=0. "Competitive reallocations" are those obeying the PV constraint, since they can be supported by selfish maximizing behavior over the life cycle, subject to a life cycle budget constraint. "Conservative reallocations" are those satisfying the Pop constraint, since in this case the set of age specific flows neither augments nor depletes the societal stock of goods, but rather conserves its level.
For transfer systems such as Social Security or child rearing, Pop(g) must be zero, since transfer systems simply reshuffle the existing output of a given time period among individuals and age groups, and are therefore conservative. But in general, PV(g) does not equal zero for transfers, so transfers are not competitive. For example, the implicit real rate of return on participation in a mature Social Security system equals n, the population growth rate, which typically is less than the real market interest rate, r, so that PV(Social Security)<0. In general for transfers, Pop(transfers)=0, PV(transfers)0. This is true for both public sector and familial transfers [3].
Now consider credit transactions. Like transfers, they involve a reshuffling of resources among age groups in any time period, and therefore Pop(credit)=0 (ignoring foreign participation in credit markets, and ignoring government debt for the moment). In this case, however, PV(credit)=0 as well, since in competitive economies, borrowing and lending take place at market interest rates. (Familial or public sector credit transactions will be viewed as part transfer when the terms diverge from market interest rates). Thus credit transactions are both competitive and conservative.
Finally, for saving and net investment (capital formation) in competitive steady state economies, PV(investment)=0, since credit markets are an alternative repository for savings from the point of view of individuals, and therefore the expected rate of interest should equal the rate of return on capital. But in steady state, the stock of capital grows at the same rate as the population (plus labor augmenting technical progress, which I ignore here), so Pop(investment)=nK>0. This, of course, is the standard result for growth of capital in steady state. Therefore investment in real capital or equity instruments is competitive but not conservative.
There is a fourth category, in which neither Pop(g) nor PV(g) is zero. In this case, some stock grows at the population growth rate but the discounted value of the age specific flows into the stock is not zero over the life cycle. This category is occupied by sums of members of other categories, such as investment plus transfers. It is also occupied by what we might call the total reallocation, given by g+(x) = consumption and g-(x) = labor earnings.
PV(g) = 0 PV(g)<>0
Pop(g) = 0 Credit Transfers
Pop(g)<>0 Capital Mixed
Every reallocation system must fall into one of these four categories; the classification system is exhaustive. This is important, because it insures that the analysis which is sketched below is general, and encompasses any means of reallocating resources across age in steady states. I will continue to name each type after the leading example of category member, but in fact there are other important members as well [4].
Consider the budget constraint of the individual at age x. The gap between labor earning, yl(x), and consumption, c(x), must equal the net inflows from transfers from family and government, plus the net in flows from credit transactions, plus net inflows from capital (see Lee, 1994b). This decomposition of the gap between labor earnings and consumption is shown for the U.S. in Figure 2 (reproduced from Lee and Miller, 1995) which plots, by age of household reference person (similar to household head), the net flows into the household for each of the three kinds of reallocation system based on the 1991 Consumer Expenditure. Patterns are easy to see above age 60: there is an enormous gap between consumption and labor earnings, and this gap is made up by the sum of transfers (largely public sector pensions and health care), credit (largely returns to bonds and money market holdings of households and their private sector pension funds), and returns to capital (a combination of household capital, principally services from owned homes and consumer durables, plus household investments in the stock market, plus payments from private sector pensions holding investments in stocks and physical assets). In the middle years, households make major transfers to others through the public sector, and they make major net payments into credit systems (paying home mortgages and buying credit instruments); on the positive side, they receive a net inflow of returns to capital, probably mainly in the form of housing services which offset their outflows of investments. Young households are net recipients of transfers, and net recipients of funds through credit (borrowing), while funds flow out to acquire capital (housing and consumer durables).
Here I have classified reallocation systems according to properties that have deep implications as we will see in a moment. But reallocations can also be cross-classified by institution, since reallocations take place within the family, the market or the public sector (see Lee, 1994a or b) [5] These institutional channels also have very important implications. In a later section, I will provide some detail on public sector transfers in some Third World nations and the US, and also on familial transfers in the U.S. (more detail can be found in Lee, 1994a and Lee and Miller, 1995).
From the various combinations of these two aggregate constraints, we can derive important formal properties of each of the four kinds of transfer system, under steady state assumptions, as follows (proofs omitted):
1. The implicit rate of return earned through any transfer system equals the population growth rate.
This result must apply to any transfer system, including familial ones such as bequests or childrearing. (E.g. if n>0, then a couple will pay out more in childrearing costs than it received as children, and it can be shown to pay "interest" at rate n on what it received.) The result follows immediately from inspection of the equation for Pop(g)=0).
2. The g(x) function for credit must cross the zero line at least twice, while for transfers and for investment, it must cross the zero line at least once.
In other words, for a credit system, there must be at least two age intervals of net borrowing (lending) separated by a period of net lending (borrowing). This is proved formally in Bommier and Lee (1995), but should be intuitively clear from the fact that a credit system must be both competitive and conservative. In any two age-group model, no credit transactions can take place between generations, because at most one cross-over is possible. The economic interpretation is simply that if generations overlap for only one period, then repayment is impossible, so no intergenerational credit transactions can take place. In a three age-group population, there can be two cross-over points, so intergenerational borrowing and lending are possible [6].
At this point, it will be useful to consider the stocks that are generated by the age specific flows that have been analyzed to this point. Define G(x) to be the present value at age x of survival weighted expected future g(x); it is the wealth held at age x through system g. Let G be the population-weighted average of G(x). G is the measure of aggregate wealth held in system g. For example, if g(x) describes a Social Security system, then G(x) is the difference between the present value of survival weighted expected future benefits and expected future payroll taxes, and is therefore Social Security wealth at age x. G is Social Security wealth per capita in the whole population. G(x) was plotted in Panel C of Figure 1.
In the remainder of the paper, G(x) will be used for the general concept, but life cycle wealth will be denoted W(x); transfer wealth by T(x); wealth held in real capital by K(x), and wealth held as credit by M(x). T(x) is the sum of familial transfer wealth and governmental transfer wealth: T(x) = TF(x) + TG(x). Governmental transfer wealth, TG(x), is very closely related to the generational accounting approach described by Gokhale in this volume; the main difference is that the taxes included in generational accounts include not ony those taxes which pay for public transfers, but also the taxes used to pay for other government expenditures such as defense, research, or investment in infrastructure, which are not age specific.
3. In the population at any instant, for any dollar of debt that one person owes, there must also be a corresponding dollar of credit that is due to someone else, so aggregate credit wealth must be equal to zero: GC=0. This can be shown to follow from the property of a credit system that PV(g)=0 and Pop(g)=0. For transfers, GT will typically be nonzero, so transfer systems can support positive or negative wealth in society as a whole. This is because transfer systems can obligate people who do not yet exist: my Social Security wealth is based in part on the obligation of children not yet born to pay taxes when they are adults. It is because of this fundamental property of transfers, in contrast to credit, that transfers can enable an economy to achieve an efficient outcome when purely market mechanisms may fail, as in Samuelson's (1958) classic example.
4. If the market interest rate equals the population growth rate,
that is in the golden rule case, then 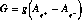 where
g is the average gross reallocation in the population (g=Pop(g+)=Pop(g-))
and A is the average age in the population at which a gross
flow takes place; for example,
where
g is the average gross reallocation in the population (g=Pop(g+)=Pop(g-))
and A is the average age in the population at which a gross
flow takes place; for example, 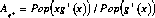 . This accounting identity states
that the wealth held through a reallocation system equals the
size of the per capita flow in the population times the difference
between the average age at which people receive inflows or benefits
from the system, and the average age at which the make payments
into the system. For example, in the case of Social Security in
the U.S., the average age of receiving a pension benefit is 71
years, and the average age of paying taxes into the system is
43 years (both for households by age of reference person), so
the difference is 28 years. This, times the average annual flow
per household of about $2500, gives an estimated Social Security
wealth per household of $70,000. This tells us that the average
household, looking forward, expects to receive $70,000 more in
benefits in the future than it expects to pay in taxes.
. This accounting identity states
that the wealth held through a reallocation system equals the
size of the per capita flow in the population times the difference
between the average age at which people receive inflows or benefits
from the system, and the average age at which the make payments
into the system. For example, in the case of Social Security in
the U.S., the average age of receiving a pension benefit is 71
years, and the average age of paying taxes into the system is
43 years (both for households by age of reference person), so
the difference is 28 years. This, times the average annual flow
per household of about $2500, gives an estimated Social Security
wealth per household of $70,000. This tells us that the average
household, looking forward, expects to receive $70,000 more in
benefits in the future than it expects to pay in taxes.
This accounting identity also suggests the graphic device of drawing arrows with a tail at the average age of paying into a system, and head at the average age of receiving from the system, and width equal to the average flow, as a way of portraying a reallocation system and the wealth it generates, which is then given by the area of the arrow, and signed by the direction of the arrow.
5. In steady states with capital, if g is the system of investing and receiving returns on the investment, then Pop(g)=nG=nK, where K is the level of capital per capita in the population. This simply states that if a reallocation does not average out to zero in the population, then the stocks to which it gives rise must grow at rate n, as does capital in neoclassical growth theory.
6. Life cycle wealth, W(x), is the amount of generalized wealth
(or debt) accumulated up to age x given the consumption age profile
c(x) and the labor earnings profile yl(x) (this is a standard
definition; see, for example, Kotlikoff and Summers, 1981). Averaged
across the whole population, this gives W, average life cycle
wealth in the population. When the interest
rate equals the population growth rate, then, 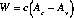 as in
the previous proposition. In any event, there is a fundamental
result:
as in
the previous proposition. In any event, there is a fundamental
result: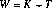 . Life cycle wealth can be held in the form of transfer
wealth (in the sense of 4 above) or capital. Capital, of course,
is productive, while transfer wealth is nothing but a symbolic
social construct which is of no physical use at all, so it is
a matter of great concern to society in which of these forms life
cycle wealth is held.
. Life cycle wealth can be held in the form of transfer
wealth (in the sense of 4 above) or capital. Capital, of course,
is productive, while transfer wealth is nothing but a symbolic
social construct which is of no physical use at all, so it is
a matter of great concern to society in which of these forms life
cycle wealth is held.
Additional results can be derived along these lines, including expressions for wealth when the interest rate does not equal the population growth rate, and also when the population and economy are not in steady state (see Bommier and Lee, 1995). The following expression for the change in wealth held through a reallocation system for non-golden rule, non-steady state economies is due to Bommier, and is proven and discussed in Bommier and Lee (1995):
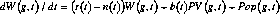
From this equation a number of useful dynamic properties can be derived, and also the expressions for average wealth held through reallocation systems of each kind can be inferred for the non-golden rule steady state case.
Let us return to the equation W = K + T which is an accounting identity, and therefore is uninformative about behavior. There is an infinite variety of behaviors that can satisfy it, so it cannot tell us how people behave. However, we can still gain some insights from interpreting it. Consider two identical stable populations with identical life cycle profiles of earning and consumption, and therefore identical W(x) functions and the same per capita wealth, W. The identity tells us the sums of transfer wealth and capital wealth must be equal. But one population could hold more of its life cycle wealth in the form of capital, and the other could hold more in the form of transfer wealth. In some sense, then, transfer wealth and capital can be thought of as substituting for one another as vehicles for satisfying the demand for life cycle wealth on the part of individuals. From the point of view of production in the macro-economy, however, they are not substitutes at all; transfers are useless. Feldstein (1974) and many others have argued that the enormous increase in transfer wealth resulting from the establishment of the Social Security system in the U.S., and the dramatic extension of its coverage and benefits, has substituted for private life cycle savings, and has therefore reduced capital formation. Barro (1974) has countered that the public sector transfer wealth through Social Security should merely have substituted for familial transfer wealth: elderly parents compensate for their increased positive public sector transfer wealth by increasing their bequests or inter vivos transfers to their children, thereby creating offsetting negative transfer wealth, leaving T and K unchanged.
Another interpretation is developed in the Lillard-Willis paper, in this volume. Consider the financing of higher education for two societies with the same life cycle profiles, the same population age distribution, and therefore the same life cycle wealth. In one, children must borrow the funds to pay for their higher education, either from the market, their parents, or the government. In the other, the parents transfer the necessary funds to their children. When education is funded by transfers, which are necessarily downwards in this case, this makes overall transfer wealth less. To maintain the equality of transfer wealth plus capital to life cycle wealth, it must be that capital is increased (which would mean, of course, that labor productivity would be higher, and the assumption of identical life cycle wealth in the two societies would be violated--but the point should nonetheless be clear). What has happened? Suppose education was funded by parental loans. Then the parents can count on repayment later as part of their provision for old age, whereas if instead they transfer the funds, then they will have to do additional saving and capital formation to provide for their old age.
For most of the societies to be considered in the next section, the only information currently available is the age profiles of labor earning and consumption. The gap between these two can in principle be decomposed into familial and public sector transfers, credit transactions, and real capital transactions, but in practice the data to do this are not yet available except for the United States. Nonetheless, consideration of the analytic framework developed earlier shows that it is possible to draw useful inferences about familial transfers from these simple life cycle profiles. First note that K must by definition be non-negative. Second, for these societies either public sector transfers are almost entirely absent, or they are not reflected in the life cycle age profiles we use. Third, note that for credit transactions, whether within the ramily or between families, the average ages of borrowin and lending in the population must be equal, and the stock of net-credit in the population must be zero (assuming the population does not hold government debt or foreign net credit. From these considerations, it follows that life cycle wealth, W, must exceed familial transfer wealth, TF. It also follows that the net direction and distance of familial transfer flows, given by the difference between the average age of receiving a gross transfer and making one, must satisfy:
A+ - A- (c/)(Ac - Ayl)
From this we can infer that if the net reallocation of resources over the lifecycle is downwards, then so is the net direction of familial transfers; if the net diretion of reallocations is upwards, it is still possible that familial transfers may be on net downwards, if the per capita capital stock is sufficiently large. If , the per capita flow of gross famillial transfers is no larger than c, per capita income, then the familial transfers will be at least as downwards in years as is net reallocation over the life cycle. These results will be used as the basis of inference about familial transfers in the next part.
While the needs and dependency of childhood have always been with us, it appears that the quantitative significance of the dependency of old age may have been a relatively new phenomenon--both because old age was rarely achieved, and because those who did achieve it often remained quite productive. Old age dependence as a general phenomenon has resulted from changes in both the demographic life cycle and in the economic life cycle. These same changes have altered childhood dependency as well--weakening it demographically, as declining fertility and lengthening life reduced the preponderance of children in the population, and strengthening it, as the industrial economy limited the economic contribution of children by rewarding extended training.
Within each population, these first and third stages of life dominate the flows of resources from those who produce a surplus to those whose consumption exceeds their output. Beyond these great tidal flows up and down the age scale there are, of course, eddies and crosscurrents as well, which largely cancel one another.
As the demography and economics of the life cycle change, it appears that the net direction of transversal resource flows changes as well. It is likely--and the evidence will be considered later--that in many if not most pre-agricultural societies, the direction of net flows was strongly downwards, from older to younger. In agricultural societies, before the demographic transition commenced, the flow was still, very likely, downwards. Although the third stage of the economic life cycle had begun to emerge in the sense that elderly people may have consumed more than they produced, the third stage of the demographic life cycle remained vestigial. During initial stages of the demographic transition, mortality declines made old age loom larger in the individual life cycle, but the same mortality declines caused a dramatic acceleration of population growth and actually made population age distributions somewhat younger rather than older; consequently from a population point of view, the first stage of the demographic transition made the third stage of the life cycle less important, not more. But when the modern industrial state cum welfare state is in full flower, then the direction of resource flows is strongly reversed, and becomes very distinctly upwards. This reversal is in part due to the changing demography, as both mortality and fertility reach low levels and the population ages, and in part due to the emergence of thorough-going retirement.
Paralleling these changes are massive institutional changes: the rise of the state and the emergence of its transfer functions; the emergence of property rights; the emergence of financial institutions and capital markets, and of insurance.
In Caldwell's (1976) classic article on demographic transition theory, he states his views on the direction of interage resource flows unambiguously:
"The key issue here, and, I will argue, the fundamental issue in demographic transition, is the direction and magnitude of intergenerational wealth flows or the net balance of the two flows--one from parents to children and the other from children to parents--over the period from when people become parents until they die....It may even be closer to the truth in the older traditional village to speak of the flow being from the younger to the older in the community as a whole with the parent-child relationships in each family playing only a secondary role....In all primitive societies and nearly all traditional societies the net flow is from child to parent." (p.140).
The anthropological literature, when it addresses the issue, is more cautious on this point. According to an old but still much cited synthetic study by Leo Simmons (1945), who reviewed a large collection of qualitative ethnographic studies on the role of the elderly, the elderly tend to get a share of general food production beyond their own contribution when there is general food sharing. General food sharing is more likely in more harsh and variable environments, and less likely when food sources are more abundant, such as in agricultural settings, and when property rights are better established. In particular, based on a survey of data from 50 to 100 groups, it appears that food sharing in general, and net food contributions to the elderly in particular, are more common in gathering and fishing groups, next most likely in hunting and horticultural groups, and least likely in agricultural groups. From Simmons' discussion, it appears that there might be systematic differences across cultural and economic groups in whether the elderly are net producers or net consumers in pre-agricultural societies. However, Simmons' sources did not attempt to quantify the productive contributions of children or the elderly in relation to their consumption.
Caldwell (1976) argues forcefully (p.141) that the qualitative assessments of informants cannot be taken at face value in this regard. Caldwell suggests that it would be very difficult to evaluate the net direction of wealth flows by examining the interactions of parents and children, because some of the transfers of resources might take place through institutional channels above the family, such as the village. One very straight-forward way to avoid this difficulty in evaluating the direction of resource flows is simply to estimate what the average person at each age produces and consumes. The difference must be some sort of reallocation across age, and as discussed earlier must be either a transfer, or a credit transaction, or capital accumulation. In many contexts, capital accumulation can be ruled out as a possibility (see Kaplan, 1994) just as Samuelson (1958) ruled it out by assumption. As already shown, credit cannot be used to reallocate resources either upwards or downwards in aggregate in a closed population, so it cannot alter the net direction of resource flows. For many societies, particularly those in which market financial institutions do not exist, and the state is an irrelevancy, any discrepancy between producing and consuming, or at least any net upwards or downwards reallocation, can safely be attributed to familial transfers. In these circumstances, it is readily shown that the difference between the average ages of receiving and giving familial transfers must exactly equal the difference between the average ages of consuming and producing.
Anthropologists have gathered detailed information on the economic activities of many small groups living by hunting and gathering, forest horticulture, and extensive agriculture (swidden). Some of these studies can provide data on time use by age and sex; others actually provide estimates of the caloric content of food gathered or grown, and food consumed. Such studies must confront many difficulties, including the ascertainment of age, determination of whether time is being used productively [7], the measurement of consumption when food is eaten from a common pot, the extreme scarcity of people at advanced ages, and varying degrees of exposure to a wider market (see Friou et al, 1995).
Kaplan (1994) has carried out one such study of forest horticulturalists in the Amazon basin which is unusually careful and detailed, and which directly addresses the question of intergenerational transfers. These groups produce food through swidden agriculture supplemented by some hunting and gathering. Kaplan's data include measures of the caloric yield of the productive activities of each individual sampled. Kaplan finds that in each of these three groups, transfers passed strongly from adults and elderly down to children, so that the net direction was downwards, contrary to Caldwell's assertions. He generously provided me with his basic aggregated data in tabular form, and I have reanalyzed it using the analytic framework and methods described earlier. Because the age profiles are quite similar for all three groups, and because the groups are all small, I grouped them together into a single population of 430.
Figure 3 presents the results. Panel A plots the population age distribution for sexes combined (the 60+ are assumed to be equally distributed in the age groups 60-64 and 65-69), which is evidently very young with median age of 15, and 59 percent under the age of 20. Panel B plots the age profiles of consumption and production. The level of the consumption profile has been proportionally adjusted so that given the population age distribution, total production equals total consumption. This is consistent with Kaplan's assertion that all output is consumed within a few days, and there is no store of value. In Panel B we note that children do not begin producing as much as they consume until age 20, echoing a conclusion of Kaplan's. Once people become net producers, they remain so (on average) for the remainder of their lives; at no point in these data do we observe the older members of the population reducing their productive output below their consumption needs. Indeed, Kaplan reports that the more children or grandchildren an older person has, the harder they work, and the more they transfer downwards.
From these data, the average ages of production and consumption can be computed [8], and they are, respectively, 34 years and 23 years. In other words, the net direction of transfers in these pooled groups is very strongly downwards from older to younger; the average calorie of food is consumed by someone eleven years younger than the person who produced it.
We would also like to be able to compute transfer wealth, W(x), at each age x and as an average in the population. To do this, we need a survivorship schedule and a discount rate. We have neither. However, when all reallocations are transfers, the appropriate discount rate is the implicit rate of return earned on transfers [9]. In a stable population, that would equal the population growth rate, as was pointed out earlier. Let us suppose for a moment that we already know the survivorship schedule, p(x). Then there are two routes by which we can find an appropriate discount rate. First, armed with p(x) we can estimate the rate of population growth from the cross-sectional age distribution [10], and use it as the discount rate. Second, again armed with p(x), we can calculate the internal rate of return to the transfer system [11], and the solution r can be used as the discount rate. In practice, the two methods give a very similar result, as they ought [12]. Panel C plots W(x) per surviving cohort member calculated using the internal rate of return. Transfer wealth becomes more and more negative as children age, reaching its minimum at just after age 20; from there on, it rises more slowly than it fell, reaching zero at the oldest age group. Thus people at every age owe transfer debt (have negative transfer wealth).
These estimates were made on the assumption that mortality corresponded to a life expectancy of 52.5 years. To see whether it matters much what mortality level we choose, I recalculated all the estimates assuming that life expectancy at birth was 35 instead of 52.5. Fortunately, the results are hardly altered at all, and certainly do not change in the least qualitatively. With higher mortality, the estimated rate of natural increase is lower, dropping from .037 to .029, and the internal rate of return is also lower, dropping from .035 to .028. The lower probability of surviving to advanced ages is almost exactly offset by the lower discount rate or rate of population growth [13].
This life cycle pattern of consumption and production could not possibly be supported by credit transactions. Adults reallocate food to their children for many years, and the children never "repay" them, since the adults remain net producers even in their old age. Recalling a theoretical result from earlier in this paper, a reallocation system g(x) must change sign at least twice if it is supported by borrowing and lending, and the g(x)=y(x)-c(x) crosses the zero line only once, at around age 20 in Kaplan's data. Nor could it be supported by capital accumulation followed by disinvestment, since according to Kaplan there are no durable stores of value in these groups, and even if there were, investment and disinvestment can reallocate resources upward to a later stage in the life cycle, but never downward to an earlier stage. In societies like these, capital accumulation could occur only if downward transfers were increased enough to sustain it, as will be discussed later.
The Human Resources Area Files (HRAF) contains monographs and time allocation data for a large number of societies, ranging from largely hunter and gatherer, through horticulturalists and intensive agriculturalists, to urban dwellers in industrial nations. The data were collected by different anthropologists for a variety of purposes, and were then coded according to a uniform scheme so that a certain degree of comparability has been attained. The time allocation studies rely mostly on the "spot check technique" developed by Allen Johnson (1975). (For further details, see Dodds et al, 1995).
The most commonly available kind of study provides data on the age/sex distribution of the population, and on the use of time in a variety of activities, of which those classified as "productive" and "housework" (see Sackett, 1989) are of interest in the present context. A research group at Berkeley, led by an anthropologist, David Dodds, has begun to analyze data for a selection of the societies in the HRAD. In an analysis to be reported below, I have grouped together data from five of these societies based on Dodds et al (1995).
The analysis was conducted exactly as that for the Kaplan data just described, except that in this case it was necessary to use the Mueller profiles of consumption by age, and productivity per hour of work by age. Use of these profiles can only be justified as a temporary expedient, until more appropriate age profiles are available. Results of this analysis are shown in Figure 4. Panel A plots the population age distribution, which is even younger than that in Kaplan's pooled data. Here the median age is 14, and 63 percent are under the age of 20. Panel B plots the age profiles of consumption and production. In these profiles, children become net producers earlier in their lives, perhaps at 14 or 15. After this they remain net producers for a very long time, but nonetheless there is a clear fall off in productivity after the mid-40s, and in the mid-60s at some point people become net consumers. The declin in production in old age is almost entirely due to Mueller's efficiency weights rather than to reduced hours of work. These profiles indicate less clearly the absence of old age dependency. Nonetheless, the average ages of producing and consuming show that the average good produced is consumed by someone seven years younger than its producer. Once again, there is compelling evidence that resources flow downwards, at least in this kind of group in this part of the world. Panel C plots life cycle transfer wealth discounted at the internal rate of return and assuming life expectancy of 52.5. The plotted W(x) shows a pattern very similar to that in the Kaplan data.
A conclusion that resources flow downwards from older to younger population members in pre-agricultural societies would be premature, since all of the groups examined are economically and geographically fairly similar. Nonetheless, I should mention that the conclusion that resources flow downward is sustained not only in these pooled data, but also for every group individually. It is my hope to extend this analysis, drawing on the file of anthropological time use studies, to other continents and to other groups producing food more exclusively through hunting and gathering. Nonetheless, the results for these populations are so strong that they may well be found more generally. In good part, the strength of the results derives from the extremely young age structure of these populations. Of course, the data on age may be unreliable, but it is hard to see how this could matter much to the qualitative results. If all ages were on average overstated by 50 percent, for example, no conclusions would be changed. All that is really needed for the results to be qualitatively right is that the ranking by age in the populations be correctly reported; absolute age does not matter much. If we continue to take the age data literally, then only about 5 percent of each of these populations is above age 50, while at least 50 percent is below age 15. Since children below 15 are net consumers in both pooled data sets, and even if those above age 50 were net consumers as well, those over 50 would have to consume enormous amounts to lead to a reversal of the downward direction of resource flows.
A paper by Sackett (1989) provides some relevant evidence covering a much wider range of societies. He has compiled a set of 105 time use studies by anthropologists for groups representing hunters and gatherers, forest horticulturalists (like those in the Kaplan and Amazonia data sets), extensive and intensive cultivators, and urban dwellers, from areas including Latin America, Africa and Asia. His general description of the age profiles of work activity is that they reach a plateau at ages 15 to 20, continuing steady into the 40s, followed by a gentle decline, reaching a level of about two thirds of the prime age adult work time at about age 65 (p.6). When he groups together what he calls "extensive" groups (hunters and gatherers, forest horticulturalists, and extensive cultivators), he finds that children in these groups tend to reach adult levels of work time later than in the intensive groups, and that the elderly tend to reduce work earlier than in the intensive groups (p.8). This description of the contributions of children appears to be quite consistent with Kaplan's data and that for the other groups in Amazonia. The description of the labor of the elderly is also very consistent with the Dodds et al Amazonia data, which show a substantial reduction already by the late 40s. The description is less consistent with Kaplan's data on the elderly, but the point is that even with the Dodds et al Amazonia profiles, which based on Sackett's work appear to be more generally characteristic of groups before intensive agriculture, the direction of transfers is very strongly downwards.
Guy Stecklov (1995) has analyzed data from the World Bank's Living Standards Measurement Survey for Cote d'Ivoire to examine the direction of interage resource flows in that population. This is the first study of a Third World national population using actual survey data specific to that country. Data include information on hours of work of various kinds for members of households in both rural and urban areas, and total labor income for the household. Stecklov used the Mueller indices of productivity per hour of work in a calculation which allocated the total household labor income to individual household members based on their hours of work. In this way he developed age profiles of output by age. Consumption was estimated by using weights estimated by Deaton (1986) to allocate total household consumption to individual members by age and sex, on a household by household basis. Then consumption by age for sexes combined was calculated by averaging across the consumption by all individuals in the sample. Details can be found in Stecklov (1995).
Figure 5 is reproduced without change from Stecklov, and shows the age profiles of consumption and production calculated separately for the urban and rural households in his sample. From these data, and data on the population which was very young and growing at 3.5 percent annually, the average ages of consumption and production can be calculated, and are 33.4 and 30.4 in rural areas. Thus once again, the direction of flows is decisively downwards, although less strongly so than in the societies previously considered.
For individuals in urban areas, the results are even more striking: the corresponding average ages are 35.4 and 24.7, for a difference of eleven years. This results from the exceptionally late break-even age for urban youth in Cote d'Ivoire. If the rural and urban data are pooled, then the overall average ages are 34.6 and 27.1, for a difference of 7.5 years.
Other data in Stecklov shows that in contrast to the Amazonian groups discussed above, in Cote d'Ivoire the hours worked falls off rapidly after the late 40s, so that even before weighting by productivity per hour, it is clear that the elderly produce much less than younger adult workers. This is true both in rural and in urban areas.
Mueller's (1976) synthetic study of production and consumption by age in peasant agriculture provides a basis for assessing the direction of transfers in a generic Third World context. Her consumption age-sex profiles are based on a survey of 9 sets of profiles in the literature, from which she has distilled profiles that she believes appropriate for poor agricultural populations in which food is the dominant item consumed. Most of her production data, and those data she draws on most strongly, refer to societies such as India and Egypt where intensive rather than extensive agriculture is practiced.
Her labor supply data were based on a review of international overview studies by Durand and the United Nations, as well as examination of census and survey data for some specific countries such as India and Egypt. These data are supplemented by data on hours worked by participant, and by a careful examination of data on the productivity of an hour worked by age and sex, based on wage data as well as other sources. From this information she constructs her overall production profiles for males and females (p.118). These profiles apply only to kinds of work that contribute to GNP as conventionally measured, and therefore exclude most kinds of home production. She evaluates these profiles as follows: "In contrast to the consumption profiles, the work-input data show a considerable degree of consistency. Despite the many weaknesses cited earlier, the work-input estimates from many countries and diverse sources have important similarities. This consistency justifies some confidence in the production profiles." (p.119) For our purposes and for hers, it is not the absolute levels of these profiles that matter. For a given population age distribution, one profile is raised or lowered in relation to the other until some target aggregate balance is achieved, such as an aggregate saving rate of 10 percent. In our case, the consumption profile will be adjusted so that total consumption equals total agricultural output.
Following Mueller, we take the population to be stable with mortality set at MWF 14 (e0=52.5) and a GRR of 3.0, leading to a an annual population growth rate of 2.9 percent. The resulting population age distribution is very young, but not so young as either of the Amazonian populations studied above. Median age is 18, with 55 percent under the age of 20. Figure 6 plots the age profiles in Panel A. Here there is clearly a life cycle stage in which the elderly consume somewhat more than they produce, but because of the young age distribution it receives very little weight. After age 65, the average person produces only about two thirds of what he/she consumes; unfortunately a more detailed breakdown by age is not available. The average age of production is 32 years and of consumption 26 years, so the direction of transfers is once again very strongly downwards from older to younger. Panel B plots life cycle wealth per original member of the birth cohort. In contrast to the data for pre-extensive agricultural societies, the third life cycle stage in which consumption falls more substantially short of production now leads to a substantial segment of the W(x) schedule in which life cycle wealth is positive--that is, after age 45 or so, the average person would expect to consume more than they produce in survival-weighted present value from there on out. Nonetheless, the overall average wealth in the population (the population weighted average of W(x)) is overwhelmingly negative.
How much are these results for Mueller's data altered if we alter the demographic assumptions? When we use a stable population with the same mortality, but with a GRR of 2 instead of 3, the growth rate drops to 1.5 percent per year, and the population becomes older. Nonetheless, the direction of transfers remains strongly downwards, with an average age of production of 35 years and consumption, 30 years. When we use a stable population with a life expectancy of 35 (MWF 7) and GRR = 3, the growth rate drops to .004 and again the population is older, but the direction of transfers remains the same: the average age of production is 36 and of consumption, 32. In other words, given the Mueller profiles and the assumption that aggregate consumption equals aggregate production among the rural peasant population, the conclusion of strong downward transfers is robust to plausible variations in demographic assumptions across steady states.
In other studies (Lee, 1994a and b), I have mainly used a household rather than individual framework for doing the accounting for the U.S., but here I will express results in the individual framework for sake of comparability. For the U.S., labor income includes pretax wages and salaries, self employment income, fringe benefits, and the employer's share of the Social Security payroll tax. Consumption includes the kinds of expenditures usually included in a household survey, except that expenditures for owner occupied housing, automobiles, and other consumer durables are treated not as current consumption but as investment, and it is the imputed services flowing from these capital goods that are counted as consumption in the years following the purchase. In addition, in-kind government transfers, particularly public education and publicly provided health services (Medicare and Medicaid) are included as consumption. Data are obtained from the 1991 Consumer Expenditure Survey (CES) and from other standard government sources. Expenditures are available only for households, not for individuals. The Lazear-Michael (1988) weights were used to estimate the share of household consumption going to each household member for each household, and then these amounts were averaged across age groups to derive a profile of consumption by age for individuals [14]. The resulting profiles differ from the earlier in that in-kind governmetn transfers and services from capital goods such as housing or cars were explicitly included.
Using the actual US population age distribution, the average ages of consuming and producing are 43 and 41, so that reallocations are upwards rather than downwards. In the stationary population, the age gap grows to four years upwards.
Figure 7 Panel A shows the age profiles that result from these calculations. The young do not become net producers until their early 20s, and the elderly become net consumers in their early 60s. Consumption rises slowly but steadily from the early 20s through the mid-60s, after which it is flat. There are two points to keep in mind in relation to this profile. First, about a quarter of consumption at advanced ages is in the form of in-kind health service transfers from the government; disregarding health transfers, the profile would slope strongly downwards. Second, the profile is cross-sectional; if labor productivity grows over time, as it has throughout most of the twentieth century, then an individual experiences more strongly rising consumption over the life cycle.
For reasons that remain unclear, it was not possible to solve for the internal rate of return when the profiles were balanced using the actual U.S. population age distribution, so a stationary age distribution was assumed instead, corresponding to a life expectancy of 75. The wealth profile, W(x), is plotted in Panel B. It can be seen that there is now a very substantial period of the life cycle in which life cycle wealth is positive, with a cross-over at around 37 or 38. Life cycle wealth peaks at about $225,000 at age 62 or 63. The population weighted average of life cycle wealth, W, is now positive.
When the calculations are instead done on a household basis, using age of household "reference person" instead of age of individual, then the difference in average ages is larger because reallocations downward to children within the family are submerged. Lee and Miller (1995) report an average age of consumption of 48.9, and of earning, 43.2, for a difference of 5.6 years, based on the actual age distribution of households, using data for 1991. Ermisch (1989) replicating an earlier study by Lee, found using household data for Japan and England that reallocations were upwards by about four years in both of those countries.
Figure 8 summarizes these data by plotting, for each group, an arrow with its tail at the mean age of production and its head at the mean age of consuming [15].
The figure tells a very clear story: for every preindustrial society examined, the direction of net transfers is downwards, usually very strongly so. It remains to be seen whether further studies of additional societies confirm this pattern, but it appears quite likely that they will. For the sole industrial society examined, the U.S., the net direction of reallocation is upwards, and as noted, Ermisch's results for England and Japan are consistent with this finding. It appears, then, that as Caldwell suggested, there has been a reversal in the direction of wealth flows--but contrary to Caldwell, wealth flows have been downward from older to younger in traditional societies, and upward from younger to older in modern societies, just the opposite of his claim.
So far we have considered neither the mechanisms nor the institutional channels through which these reallocations are channeled. Recall, however, that it was shown at the end of the earlier theoretical part of the paper that for these preindustrial data sets we can conclude that downward reallocations overall imply that familial transfers were correspondingly downward.
For industrial societies, the situation is rather different because of the importance of capital and the importance of public sector transfers. Separating familial transfers, Tf, and governmental transfers, both financial and in-kind, Tg, we have: Tf = W - K - Tg. We have seen that W is positive, and that reallocations in general are upwards by about four years. But, as we shall see in the next section, both K and Tg are very substantial positive values, so that in fact familial transfers in the U.S. are strongly downward, just as in the other societies examined. The reversal of the direction of net reallocations does not correspond to a reversal of the direction of transfers within the family. The structure of these downward familial transfers in the US will be examined in more detail later.
So far I have shown that the direction of net reallocations is strongly downwards in all preindustrial settings I have examined. But perhaps it is not clear that this concept of the direction of "wealth flows" is directly relevant for the fertility decision, so I will also do a rough and speculative calculation which bears more directly on the Caldwell theory of incentives for childbearing in relation to the direction of flows.
Consider a young adult deciding whether to have an incremental child. The mean age at childbearing can be taken to be 30, so we will imagine a 30 year old facing this decision. The only data at hand, let us suppose, are the average age profiles, and mortality and fertility. From these alone we cannot infer the result of some perturbation to the system in which these age profiles are embedded. For example, if a parent decides to have one more child, that child might be given the average amount of consumption of the preexisting children or alternatively, the total consumption allotted to children in the family might remain constant, and the share going to each child might therefore be reduced. At the same time, the parent might increase his/her hours of work to provide income for increased familial consumption, or the consumption of all household members might be somewhat reduced to provide for the incremental child. The literature contains empirical evidence on some of these possibilities (Chayanov, 1965, on the response of family labor and consumption, and Deaton and Muelbauer, 1975, and Lazear and Michael, 1988, on how the consumption of family members changes in the presence of an incremental child, for example). Because the marginal utility that the parent gets from leisure should equal parental marginal utility from familial consumption, all these different scenarios of adjustments to an additional child should entail equal costs, so it should not matter which we evaluate [16]. It will be simplest to assume that the parent increases hours of work in order to generate the additional income to enable the incremental child to consume at the same rate that pre-existing children do. There is a similar problem at the other end of the age range: if the parent has an additional child, will that child transfer to the parent at the average rate of the child's siblings, or will each child reduce the transfer so that the total transfer to the elderly parent remains unchanged while the burden on the children is reduced? One might suppose that this question is linked to the previous: if each incremental child is treated exactly like the preexisting children, then it will transfer to the parent exactly as the preexisting children do. This, at any rate, is the assumption that I will make in trying to derive a measure of the costs and benefits of an incremental child from the consumption and earning profiles.
We can take the net cost of a child to be the integral under the (yl(x) - c(x)) curve, weighted by survival p(x), over the range in which consumption exceeds output. We can take the return to all childbearing, from the point of view of the parent, to be the transfers received at older ages which permit consumption to exceed earnings; this will again be given by the integral under the (yl(x) - c(x)) curve, weighted by survival p(x), over the range in which it is negative at old ages. However, since the adult will not be in a position to make a fertility decision unless he/she is alive, we can assume that age 30 was attained, and condition on survival to this point. The returns to childbearing should then be as just described, but divided by p(30). Further adjustment is necessary, since the costs incurred to receive these familial transfers in old age are not the costs of one child, but the costs of half of all children (since there are two parents).
Taking these various factors into consideration, the costs and benefits of bearing an incremental child should be related to the age profiles of consumption and production as follows:
Net Cost of Child (NCC): 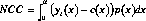
Return per Child (RPC): 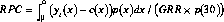
where is the age at which a child breaks even, with earnings equal to consumption, and is the age at which an older person again just breaks even, with falling earnings intersecting the consumption curve.
For the groups studied by Kaplan (1994) this whole line of analysis is irrelevant, since there is no period in the life cycle in which adults are consuming more, on average, than they are producing. For the Mueller profiles with e0 = 52.5 and GRR = 3.0, the calculations come out as follows: NCC = 2.55 units; RPC = .25 units; ratio of RPC to NCC is .1. In other words, a parent can expect to get back in old age support from an incremental birth about one tenth of what they spend to rear that birth. One might argue that it is wrong to weight this amount by the probability of surviving to the age at which the support would be received, since it is a kind of insurance against the contingency of survival. If we condition the return on surviving from age 30 to age 65, it becomes larger by a factor of (p(30)/p(65)) which in the present case is about 1.6. In this case, a parent who survived to age 65 would receive from each child about one sixth of what had been invested in each child.
I have also calculated the implicit rate of return that is earned on the expenditure on children in this example, which is -.067 per year. This is based on the calculated return of one tenth of what has been invested, and taking account of the gap between the average age of investing in a child, which is 30 + 8, or 38, and the average age of receiving a return transfer, which is 73, for a gap of 35 years. If there is economic progress such that the age schedules for consumption and production shift upward at some annual rate, then that rate would be added to the calculated rate of return. For example, if there were progress at three percent per year, then the average annual rate of return would rise from -.067 to -.037. In sum, bearing children is an extremely costly way of providing for old age, yielding far less in old age transfers than it costs, so that the rate of return is strongly negative [17].
I believe that these data and calculations demonstrate that wealth does not flow upwards in the traditional societies examined here. I believe that this assertion by Caldwell is mistaken. But Caldwell's main point, that high fertility is economically rational for one or both parents in traditional societies, does not require that wealth flow upwards in my view. In the absence of institutions providing various kinds of insurance and which permit the reallocation through savings of resources to old age, children may still be the best deal around [18], although the extent to which assets such as land or livestock might fulfill the same functions is unclear. Lillard and Willis;Wu; and Nugent (all in this volume) all provide evidence of upwards transfers from older children outside the parental home to their parents, but it is highly doubtful that these would be large enough to offset the costs of childrearing incurred by their parents earlier.
Capital accumulation has two effects of interest here: first, capital is productive, and its presence raises the productivity of labor and raises total output; second, the accumulation of capital defers consumption, since it is necessary to forego consumption of some output today in order to create the capital; and it raises consumption in the future when the returns to capital are received. (In Austrian capital theory, the returns to capital were viewed as a reward for waiting.) Thus capital has both a productive function and a reallocative function. But one might want to accumulate capital for efficiency in production (farm animals, farm machinery, land, and so on) but not want to defer consumption. Or one might want to defer some consumption until old age, but have no need for productive capital. For an individual, the link between deferring consumption on the one hand and acquiring productive capital on the other can be broken by borrowing the money necessary to pay for the capital. But for a society as a whole this is not possible, since the stock of debt must equal the stock of credit (unless one borrows from foreigners or government debt is issued). For a society as a whole, if it is limited to purely market mechanisms, then the stock of capital must just equal life cycle wealth, W; and life cycle wealth, since it must necessarily equal the value of the capital stock which must be non-negative, must itself be non-negative. But in reality no society is limited to purely market mechanisms, and transfers, at least to children, are always present. Transfer wealth T breaks the link between capital accumulation and waiting at the societal level. K no longer need equal W.
The theory of life cycle saving asserts that the desire to provide for net consumption in old age is the main motivation for saving and capital formation, and therefore is the underlying explanation for the accumulation of wealth (Modigliani, 1988). But we have seen that in all the preindustrial societies we examined, life cycle wealth is actually negative--that is, the average person in the population desires to hold negative wealth, or debt, in order to achieve consumption smoothing over the life cycle. How, then, is it possible for such societies to have any capital stock at all, and can these circumstances be reconciled with the life cycle saving theory? [19]
First, it is important to recall that in every society, there are strong familial transfers to children. When a household framework is used for the accounting of interage resource flows, then the transfers to children do not enter into the total since they are mostly intra-household transfers. To some degree, the downward transfers we find in these societies are simply reflecting the downward transfers to children. If the downward transfers to children are sufficiently large, then we might well have T<W, so that W - T = K > 0. But even if transfers to young children are not sufficiently large to offset negative W, capital accumulation may still be achieved.
In the case of the Amazon Basin horticulturalists, we are told by Kaplan (1994) that K=0 and can infer that W=T<<0. Here there is nothing to discuss about the substitution of K and T. In the agricultural societies, however, we appear to have W<<0, T<<0. However, K is held in the form of land, live stock, and gold jewelry, for example, so K>0 and we can infer that T<W<<0. How are we to think of the substitution of K and T in this kind of setting? How does there come to be capital at all when life cycle wealth is negative? There are several different possibilities. First, adults may accumulate some assets during their years of net production, with the plan of drawing them down during their older years. This would be life cycle saving. In this case, they are using capital to support consumption in excess of production in their later years, and this is clearly an alternative to achieving the same result through transfers. This strategy of life cycle saving would therefore reduce or eliminate some older years that would otherwise necessarily have T(x)>0, given the assumption that production and consumption profiles are held fixed. In this way, K substitutes for T. Second, older people might avoid drawing down their assets, and instead pass them on as bequests to their children when they die. In this case, the positive K is exactly offset by a decrease in T (T becomes more negative), due to the downward flow of bequests, and again K and T substitute for one another. Third, older people might make greater transfers to young adults, in excess of the net consumption needs of young adults, permitting them to accumulate capital of their own (as in a dowry, or help to acquire a farm, a house, or some live stock). Once again, K increases and T decreases (becomes more negative).
Of course, in most forms K not only serves as a store of value (as with gold jewelry which is not worn), but is also a productive asset which raises the productivity of labor (as with land or livestock). This makes the assumption of fixed production and consumption profiles unrealistic, which is of course the reason for Feldstein's concern about the effects of Social Security to begin with.
Except for some age profiles for the U.S. that were used earlier to illustrate the main concepts of reallocation systems, the empirical work reported in this paper has been limited to examining the age patterns of labor earnings and consumption, and their difference. Figure 2 decomposed the gap between these two age profiles into net flows through each of the major kind of reallocation system: transfers, credit, and investment in capital. Unfortunately, nothing similar has yet been done for countries other than the U.S., so comparative results cannot be reported in any general way. However, there are two specific kinds of transfer systems for which some comparison is possible. First, I will present comparative results on public sector transfers in some Third World countries and the U.S. Second, I will present some results on familial transfers in the U.S. which may be roughly compared to the earlier results on production and consumption profiles in preindustrial societies, which I argued must reflect almost exclusively familial transfers.
Not surprisingly, the industrial welfare states devote a substantially greater proportion of national income to public sector transfers, both in cash and in kind, than do typical Third World countries. For example, India in recent years has devoted about 4 percent of GNP to public expenditures on health, education and pensions, of which nearly two thirds has gone for education, and only ten percent for pensions. The US, by contrast, has spent about 15 percent of GNP, or four times India's share, on such transfers, of which 36 percent was for education, while about 35 percent was for pensions.
The difference is not just in the scale of public sector transfers, but also in their allocation by age. The industrial nations have far higher proportions of elderly in their populations than the Third World nations. In the U.S., for example, at the current vital rates, the stable population would have a ratio of children to the elderly about one twentieth as high as Kenya's. This purely demographic difference would tend to make the economic burden of supporting the elderly more important in industrial nations. However, this is only half the story. In most Third World countries, care and support for both children and the elderly are largely family matters. In industrial nations, by contrast, while the rearing of children remains primarily a family obligation, the elderly are increasingly supported by the public sector through income transfers (pensions) and through in-kind transfers of health services. In the US, an average elderly person receives net public transfers costing roughly 3.7 times as much as does an average child. In India, Bangladesh, Kenya and Saudi Arabia, the same ratio is between .6 and .8 (see Lee, 1991b). Taking into account these differences in age distribution and in the scale of transfers, in the U.S. an elderly person receives annual transfers equal to 59 percent of per capita GNP, while in Bangladesh, the corresponding percentage is 1.8 percent. In the hypothetical U.S. stable population, more than 10.6 percent of GNP would be transferred to the elderly, while in none of the four Third World countries in Africa and Asia I examined would this be more than .5 percent, and in Kenya and Bangladesh, it would be less than .2 percent (Lee, 1991b). The situation is doubtless quite different for some Latin American countries with strong public sector pension programs, such as Brazil. It appears that in Brazil, the average elderly person receives perhaps fifteen times as much as the average child from the public sector, a ratio that is many times higher than prevails even in the industrial nations (Lee and Miller, 1990). Throughout Latin America there is growing interest in converting the Pay As You Go public pension programs to funded public programs (see Rofman in this volume and Salvadore *** in this volume.
It is instructive to consider the population weighted age profiles of public sector transfers for India circa 1981, which appears to be fairly typical of Third World nations in this regard; these are plotted in Figure 9. It is clear from the figure that transfers are on average received at a younger age than are the taxes which support them, and calculations reveal that the gap in average ages is eleven years downward. Similar calculations for a number of other Third World nations show a similar pattern--for example, public sector transfers were downward by eleven, thirteen and fourteen years, respectively, in Bangladesh, Saudi Arabia and Kenya. However, for Brazil, the net direction of transfers was upwards, despite a relatively young population age distribution, due to the importance of pensions (Lee and Miller, 1990). In the U.S.--and most likely the situation is similar in all industrial nations--the net direction of public sector transfers is strongly upwards, by ten years.
The downward direction of public transfers in most Third World nations is a source of negative externalities to childbearing, since a younger age distribution is costly to the public but these costs are not incurred by the individual parents considering bearing a child (Lee and Miller, 1990). Similarly, the upward direction of public transfers in the U.S. and probably in other industrial nations is a source of positive externalities to childbearing, since a younger age distribution is beneficial to the public, reducing the per worker costs of supporting the elderly, but this benefit does not accrue to the individual parent. In most Third World nations, the size of the negative externality arising in this way is fairly small relative to per capita GNP. For example, in India, Bangladesh, Saudi Arabia, Kenya and Mexico the fraction is -.1, -.04, -.2, -.2, and -.1, respectively. In Brazil, however, it is positive at +.25, and in the U.S. it is more than two! (See Lee and Miller, 1990).
I have reported that the overall direction of reallocation over the life cycle is downward in all preindustrial populations I have examined, and upwards in all industrial populations I have examined. But this is somewhat misleading, particularly when considered in conjunction with fertility theory. The fact is that in the U.S., reallocations are strongly upwards through capital accumulation and through public sector transfers, but they are strongly downward through the family, just as they are in every other society examined in this paper. In the U.S., not only do parents make downward transfers to their young children as appears generally to be the case, but the elderly also make downward familial transfers, on net, to their adult children. (It should be noted, however, that this net downward direction of transfers from the elderly might look quite different if the value of the time spent by adult children in caring for their elderly parents were included.)
Figure 10 uses an arrow diagram to portray four kinds of net transfers within the family based on U.S. data. Child costs is a measure of the average direct costs of rearing a child through age seventeen, net of their labor earnings. The flows to children are calculated as described earlier for the consumption profile. The tail of the arrow is located at the average age of the parent making the transfer, and the head of the arrow is located at the average age of the child receiving the transfer. The thickness of the arrow represents the average flow to children per member of the total population, and the area of the arrow is then the average total cost of a child (discounted at the population growth rate, here taken to be zero). This total cost was $80,000 in 1987, and constitutes negative transfer wealth. The arrow for private expenditures on higher education is similarly constructed, and indicates negative transfer wealth of $6000. Together these indicate a net transfer to children while they are young of $86,000 per birth; this amount also measures the direct cost of a child. Note that if we assumed that costs of a child were rising at, say, three percent per year, and we also discounted at three percent per year, then the result would remain exactly the same. The other panel shows familial transfers that flow between households. These include inter vivos gifts and transfers, which generate negative wealth of $5500 per household, or about $2000 per individual. These are doubtless seriously underreported in the Consumer Expenditure Survey, and should be considerably larger. Finally, bequests constitute a very important downward flow at the end of life. Their measurement has been highly controversial (Modigliani, 1988; Kotlikoff, 1988), but I believe that the arrow in the diagram reflects a reasonable interpretation of the data (see Lee, 1994a for further details). The arrow indicates a downward flow generating negative bequest wealth of about $44,000 per household, or $17,000 per person in the population. For some purposes one might want to consider these transfers to adult children as a portion of the total cost of children.
Reallocation of resources from one age group to another is a pervasive phenomenon in all societies. Patterns of reallocations have important implications in a number of areas, ranging from an understanding of the societal accumulation of wealth, through theories of fertility, to the consequences of population aging. While there are many important studies of one or another specific reallocation system, such as bequests, savings, or government transfers, there seems to have been very little systematic attempt to understand the underlying patterns of reallocations as a whole, either theoretically or empirically. While theoretical work has been profound and influential, the demographic foundations of the work have been so highly stylized as to limit the problems which can be examined and empirical applications that might be made. This paper has sketched a conceptual framework that has been developed in more detail elsewhere, and then explored the patterns of transfers in several societies with different kinds of economic bases, to the extent that the limited data permit.
While the empirical basis for generalization is still very restricted, there is a consistency in findings so far. In small horticulturalist/hunter gatherer groups and societies practicing extensive and intensive agriculture, reallocations of resources over the life cycle appear to be strongly downward from older to younger members of the population, contrary to what has often been suggested, particularly in relation to fertility theory. Notional life cycle wealth in these societies, averaged over the population as a whole, is negative: the need for providing for consumption in childhood strongly dominates the need, if any, for providing for dependent old age. This situation changes for industrial societies, or at least for the U.S., where the direction of transfers is upwards from younger to older. Although transfers within the family remain strongly downward as in other societies, these are now more than offset by capital accumulation which reallocates consumption to older ages, and by strong upward transfers through the public sector. It appears that in most but not all Third World nations, public sector transfers are strongly downward from older to younger, in part because of the preponderance of children in these populations, and in part because the elderly are still sustained through familial transfers while in industrial nations the state has largely taken over this role. These differences have implications for capital accumulation, for fertility theory, for externalities to child bearing, and for the consequences of population aging.
[1] There are some important exceptions, in which an n-age group population is considered, as in Gale (1973) and Willis (1988). Neither of these articles includes non-trivial mortality, however. Arthur and McNicoll (1978) develop and analyze a model with continuous age distribution and realistic mortality; the analytic framework for this paper owes a good deal to their analysis, and to Willis (1988).
[2] There are a handful of examples of computable general equilibrium models with overlapping generations which consider the n-age group case, sometimes with non-trivial mortality, as in Auerbach and Kotlikoff (198* Dyanmic Fiscal Policy).
[3] Actually, the rate of return on a transfer system equals the population growth rate plus the rate of growth of labor productivity.
[4] For example, government debt in a steady state economy falls into the category of transfer, although this is not immediately obvious, since debt grows in proportion to the population and since the government must pay the market rate of interest to those who hold it. However, we must also include the taxes levied to pay interest on the debt as a part of the reallocation system, and the new debt which is issued so that total debt grows at rate n. Once we do, we can see that taxes must equal the difference between the population growth rate and the interest rate, times the value of outstanding debt. Viewed as a whole, the system of issuing debt, and taxing to pay interest to its holders, can be seen to fall in the category of transfers (Pop(taxes, interest)=0; PV(taxes, interest) 0). Fiat money also has transfer like properties, as shown in Samuelson, 1958.
[5] There may be additional institutions through which reallocations take place, such as charitable institutions or clans.
[6] Without kids, the credit market can clear only if some working age group, probably the youngest, is induced by negative interest rates to consume in excess of earnings--see Samuelson's (1958) three age group example.
[7] Are teenage boys, accompanying women and girls on a gathering expedition, and providing some protection by their presence as they play games, engaged in productive activity? (Example due to E.A. Hammel).
[8] If N(x) is the population at age x, then the average age of production, for example, is xN(x)y(x)/N(x)y(x).
[9] The discounting actually has a demographic role and interpretation, expressing the fact that the relation between any period of net consumption in old age that is shown by the age profiles of earning and consumption is not resulting from transfers from a single birth, but rather from all children combined, and must be set against the costs incurred in raising all children born, including both survivors and those who died before attaining the age of making transfers to their parents (the consumption of the children should be divided in two, if we are thinking in terms of the return to the average individual parent).
[10] In a stable population, N(x) is proportional to exp(-nx)p(x), where n is the stable population growth rate. Dividing both sides by p(x) and taking the natural logarithm yields: ln(N(x)/p(x)) = k - nx. In a stable population, this would be an identity. In a nonstable population we may first plot the dependent variable against age to see if the relation is roughly linear, and if so, we can then estimate n through a regression. The estimated value of n can then be used as the discount rate. In the pooled data from Kaplan, the plotted relationship does appear linear for assumed mortality of MWF 7 and 14 (e0=35 and 52.5), so regression estimates were computed as reported below.
[11] The internal rate of return solves for r in the equation: p(x)[y(x)-c(x)]exp(-rx) = 0.
[12] For example, assuming life expectancy at birth of 35 years, the estimated rate of natural increase is .0292 and the estimated internal rate of return is .0283. For e0=52.5 years, the corresponding estimates are .0372 and .0349.
[13] If we knew the fertility level, and if we were willing to assume that the populations are closed and stable, then we could estimate the mortality level and the population growth rate. For example, with e0=52.5 and n=.0372 as estimated, the implied level of fertility would be a TFR of 7.75 (based on Coale-Demeny MWF 7 stable population). Kaplan (1994) estimates the TFR to be somewhat higher than this, at 8.2 or so, for the groups he studies. At e0=35 and n=.0292, the implied TFR would be 8.6. Kaplan reports (footnote 9, p. 786) that 28 percent of the Ache reached age 60, and that this was about half the fraction that reached age 20. These figures are in very close agreement with MWF 7, e0 = 35, in Coale Demeny tables, which gives .29 reaching 60 and .60 reaching 20. Thus the scenario with e0 = 35, n = .0292, and TFR = 8.6 agrees very well with the data Kaplan reports.
[14] There are many difficulties in such an allocation of consumption to individuals; these are discussed in Lee, 1988 and 1994a.
[15] Ordinarily in this kind of diagram, used for comparisons within a given population, the thickness of the arrow would indicate the size of the annual per capita flow in the population, and then the area of the arrow, the product of its length and its thickness, would equal the per capita wealth averaged across all ages. But in these cross cultural comparisons, nothing would be gained by depicting the thickness of the arrows which would depend only on differences in per capita consumption between the societies and on the monetary units used.
[16] That is, in either case, the parent with an incremental child would have to be compensated by the same increase in income to induce the level of parental consumption of goods or of leisure that prevailed in the absence of the child.
[17] I am unable to relate these expressions and results explicitly to the calculated direction of reallocations, although I believe the two to be closely connected.
[18] Didier Blanchet (personal communication) has illustrated this point neatly with a model in which risk averse parents improve their welfare by having children who provide insurance, even though the direction of wealth flows is strongly downwards.
[19] There is considerable doubt that saving in poor agricutural societies is motivated by the life cycle needs rather than precaution; see Deaton, 199*.
Arthur, Brian W. and Geoffrey McNicoll (1978) "Samuelson, Population and Intergenerational Transfers," International Economic Review, vol. 19, no. 1 (February), pp. 241-246.
Auerbach, Alan J. and Laurence J. Kotlikoff (1987) Dynamic Fiscal Policy (Cambridge University Press, Cambridge).
Auerbach, Alan J., Jagadeesh Gokhale, and Laurence J. Kotlikoff (1991) "Generational Accounts: A Meaningful Alternative to Deficit Accounting," in David Bradford, ed., Tax Policy and the Economy (MIT Press, Cambridge, for the National Bureau of Economic Research), pp.55-110.
Barro, Robert J. (1974) "Are Government Bonds Net Wealth?," Journal of Political Economy v.28, n.6 (November/December), pp.1095-1117.
Bommier, Antoine and Ronald Lee (1995) "Continuous and Dynamic Overlapping Generations Models," unpublished manuscript of the Department of Demography, University of California, Berkeley.
Caldwell, John C. (1976) "Toward a Restatement of Demographic Transition Theory," Population and Development Review, reprinted as Chapter 4 of John Caldwell (1982) Theory of Fertility Decline (Academic Press) 113-180.
Coale, Ansley and Paul Demeny (1983) Regional Model Life Tables and Stable Populations (New York: Academic Press).
Deaton, Angus and John Muelbauer (1986) "On Measuring Child Costs: With Applications to Poor Countries," Journal of Political Economy v.94, n.4 pp.720-744
Diamond, Peter A. (1965) "National Debt in a Neoclassical Growth Model," American Economic Review, v. 55, pp.1126-50.
Dodds, David, Diana Friou, and Carl Mason (1995) "Work Time and Age-Related Wealth Transfer in Amazonia: A Review of Time Allocation Data for Six Societies." unpublished manuscript of the Department of Demography, Berkeley, California.
Ermisch, John (1989) "Intergenerational Transfers in Industrialized Countries: Effects of Age Distribution and Economic Institutions," Journal of Population Economics 1:269-284.
Feldstein, Martin (1974) "Social Security, Induced Retirement, and Aggregate Capital Formation," Journal of Political Economy v.82.
Fricke, Thomas E. (1990) "Darwinian Transitions? A Comment," Population and Development Review v.16 n.1 (March) pp.107-119.
Gale, David (1973) "Pure Exchange Equilibrium of A Dynamic Economic Models," Journal of Economic Theory 6, 12-36.
Hurd, Michael (1990) "Research on the Elderly: Economic Status, Retirement, and Consumption and Saving", Journal of Economic Literature v.28 n.2 (June) pp.565-637.
Johnson, Allen (1975) "Time Allocation in a Machiguenga Community," Ethnology v.14 pp.301-310.
Kaplan, Hillard (1994) "Evolutionary and Wealth Flows Theories of Fertility: Empirical Tests and New Models," Population and Development Review v.20 n.4 (December) pp.753-791.
Keyfitz, Nathan (1985) "The Demographics of Unfunded Pensions," European Journal of Population v.1 pp.5-30.
Keyfitz, Nathan (1988) "Some Demographic Properties of Transfer Schemes: How to Achieve Equity Between the Generations," in Ronald Lee, W. Brian Arthur and Gerry Rodgers, eds., Economics of Changing Age Distributions in Developed Countries (Oxford University Press) pp.92-105.
Kim, Oliver and Robert Willis (1982) "The Growth of Population in Overlapping Generation Models", unpublished manuscript of the Economic Research Center/NORC of the University of Chicago.
Kotlikoff, Laurence J. and Lawrence H. Summers (1981) "The Role of Intergenerational Transfers in Aggregate Capital Accumulation", Journal of Political Economy v.89, pp.706-732.
Kotlikoff, Laurence J. and Lawrence H. Summers (1988) "The Contribution of Intergenerational Transfers to Total Wealth: A Reply," in Denis Kessler and Andre Masson, eds., Modeling the Accumulation and Distribution of Wealth (Oxford: Clarendon Press), pp. 53-67.
Lazear, Edward P. and Robert T. Michael (1988) Allocation of Income Within the Household (University of Chicago Press, Chicago and London).
Lee, Ronald D. and Shelley Lapkoff (1988) "Intergenerational Flows of Time and Goods: Consequences of Slowing Population Growth," Journal of Political Economy v.96 n.31 (June), pp.618-651.
Lee, Ronald D. (1980) "Age Structure, Intergenerational Transfers and Economic Growth: An Overview," in George Tapinos, ed., Revue Economique: special issue on economic demography, vol. 31, no. 6 (November), pp. 1129-1156.
Lee, Ronald D. "Population Policy and Externalities to Childbearing," Annals of the American Academy of Political and Social Science, special issue edited by Samuel Preston World Population: Approaching the Year 2000 (July 1990), pp. 17-32.
Lee, Ronald D. (1994a) "Population Age Structure, Intergenerational Transfers, and Wealth: A New Approach, with Applications to the U.S.," with the assistance of Timothy Miller; in Journal of Human Resources v.XXIX, n.4, (Fall, 1994) special issue edited by Paul Gertler on The Family and Intergenerational Relations, pp.1027-1063.
Lee, Ronald D. (1994b) "The Formal Demography of Population Aging, Transfers, and the Economic Life Cycle," in Linda Martin and Samuel Preston, eds.; The Demography of Aging (National Academy Press, 1994) pp.8-49.
Lee, Ronald D.(1994c) "Fertility, Mortality and Intergenerational Transfers: Comparisons Across Steady States," in John Ermisch and Naohiro Ogawa, eds, The Family, The Market and The State (Oxford University Press), pp.135-157.
Lee, Ronald D. and Timothy Miller (1990) "Population Growth, Externalities to Childbearing, and Fertility Policy in the Third World," Proceedings of the World Bank Annual Conference on Development Economics, (1990, Supplement to The World Bank Economic Review and to The World Bank Research Observer, pp.275-304.
Lee, Ronald D. and Timothy Miller (1995) "Interage Resource Flows in the U.S.: A Descriptive Account" paper presented at the 1995 Annual Meetings of the Population Association of America in San Francisco.
Mason, Andrew (1987) "National Savings Rates and Population Growth: A New Model and New Evidence," in D. Gale Johnson and Ronald Lee, eds., Population Growth and Economic Development: Issues and Evidence (University of Wisconsin Press) pp.523-560.
McCandless Jr., George T. with Neil Wallace (1991) Introduction to Dynamic Macroeconomic Theory: An Overlapping Generations Approach (Cambridge: Harvard University Press).
Modigliani, Franco (1988) "Measuring the Contribution of Intergenerational Transfers to Total Wealth: Conceptual Issues and Empirical Findings," in Denis Kessler and Andre Masson, eds., Modeling the Accumulation and Distribution of Wealth (Oxford: Clarendon Press), pp. 21-52.
Morgan, James (1983) 'The redistribution of income by families and institutions and emergency help patterns,' Chapter 1 in Greg Duncan and James Morgan (1983) Five Thousand American Families--Patterns of Economic Progress, v.X: Analyses of the First Thirteen Years of the Panel Study of Income Dynamics, Institute for Social Research, Ann Arbor, 1-59.
Mueller, Eva (1976) "The Economic Value of Children in Peasant Agriculture," in Ronald Ridker, ed., Population and Development: The Search for Interventions (Baltimore: Johns Hopkins Press), pp.98-153.
Preston, Samuel (1982) "Relations Between Individual Life Cycles and Population Characteristics", American Sociological Review v.7, n.2 (April) pp. 253-264.
Sahlins, Marshall (1972) Stone Age Economics (Aldine-Atherton: Chicago).
Samuelson, Paul (1958) "An Exact Consumption-Loan Model of Interest With or Without the Social Contrivance of Money," Journal of Political Economy, vol. 66, no. 6 (December), pp. 467-482.
Samuelson, Paul (1975) "The Optimum Growth Rate for Population," International Economic Review, v.16, n.3 (October), pp.531-
Samuelson, Paul (1976 "The Optimum Growth Rate for Population: Agreement and Evaluations," International Economic Review, v.17, n.2 (June), pp.516-525.
Simmons, Leo (1945) The Role of the Aged in Primitive Society (New Haven, Yale University Press)
Starret, David (1972) "On Golden Rules, the 'Biological Rate of Interest', and Competitive Efficiency," Journal of Political Economy, 80, 276-291.
Stecklov, Guy (1995) "Intergenerational Resource Flows in Cote d'Ivoire: An Empirical Analysis," paper presented at the May, (1995 Annual Meetings of the Population Association of America, San Francisco.
Turke, Paul W. (1989) "Evolution and the Demand for Children," Population and Development Review v.15 n.1 (March) pp.61-90.
U.S. Bureau of the Census (1990) Statistical Abstract of the United States: (1990 (110th edition.) Washington, DC.
Willis, Robert (1987) "Externalities and Population," in D. Gale Johnson and Ronald D. Lee, eds., Population Growth and Economic Development: Issues and Evidence (University of Wisconsin Press), pp.661-702.
Willis, Robert (1988) "Life Cycles, Institutions and Population Growth: A Theory of the Equilibrium Interest Rate in an Overlapping-generations Model," in Ronald Lee, W. Brian Arthur and Gerry Rodgers eds., Economics of Changing Age Distributions in Developed Countries (Oxford University Press), pp.106-138.
Notes and Titles for Figures
***************************************************************
Figure 1. An Example of a Reallocation System: Social Security in the U.S., 1991
A. Gross Reallocation Schedules: Social Security Benefits and Taxes
B. Net Reallocation Schedule: Social Security Benefits minus Taxes
C. Social Security Wealth, Discounted at r=.04
Note: Based on the 1991 Consumer Expenditure Survey. The tax schedule has been adjusted proportionately to make total payroll taxes equal total benefits given the actual population age distribution. For details, see Lee and Miller, 1995.
*****************************************************************
Figure 2. How the Three Kinds of Reallocation System Make up the Gap Between Consumption and Labor Earnings for U.S. Households (1991)
Note: Based on the 1991 Consumer Expenditure Survey. For details, see notes to Figure 7 and Lee and Miller, 1995.
*************************************************************
Figure 3. Interage Resource Reallocations for Kaplan's Horticulturalists (Pooled)
A. Population Age Distribution for Kaplan's Horticulturalists (Pooled)
B. Age Profiles of Consumption and Production for Kaplan's Horticulturalists (Pooled)
C. Life Cycle Wealth for Kaplan's Horticulturalists (Pooled)
Note: A general description of the means of calculation and the data source is given in the text; for further details, see Kaplan (1994).
********************************************************
Figure 4. Interage Resource Reallocations for Other Amazonia Horticulturalists (Pooled)
A. Population Age Distribution for Other Amazonia Horticulturalists (Pooled)
B. Age Profiles of Consumption and Production for Other Amazonia Horticulturalists (Pooled)
C. Life Cycle Wealth for Other Amazonia Horticulturalists (Pooled)
Note: A description of the means of calculation and data source is given in the text. For further details, see Dodds et al (1995).
***********************************************************
Figure 5. Age Profiles of Consumption and Labor Earnings in Cote d'Ivoire
Note: This figure is reproduced from Stecklov (1995) to which the reader is referred for details; for a general description of the methods and data source, see the text.
***********************************************************
Figure 6. Interage Resource Reallocations for a Typical Rural Population Practicing Intensive Agriculture (After Mueller)
A. Age Profiles of Consumption and Labor Earnings in a Typical Population Practicing Intensive Agriculture
B. Life Cycle Wealth in a Typical Population Practicing Intensive Agriculture
Note: For a description of data and method, see text and Mueller, 1976.
**************************************************************
Figure 7. Interage Resource Reallocations for the U.S., 1987
A. Age Profiles of Generalized Consumption and Labor Earnings for U.S. Individuals, 1987.
B. Life Cycle Wealth for U.S. Individuals, 1987
Note: Data come from the 1987 Consumer Expenditure Survey, supplemented by data on public education from the U.S. Statistical Abstract and from the Survey of Health Expenditures. Labor earnings are pretax and include the employer's contribution to payroll tax and benefits, as well as self-employment income. Consumption includes conventional household expenditures, less expenditures on purchases of homes, cars and consumer durables, plus the imputed flow of services from these. The resulting household consumption is then allocated to individuals in the household using the Lazear-Michael (1988) method and estimated coefficients. Then in-kind government transfers of education and health care are added to each age as appropriate. Then the age profile of labor earnings was inflated by a factor which was calculated to equate the population weighted total of labor earnings and consumption. The population used for equalizing generalized consumption and labor earnings was the stationary (life table) population for the U.S. with e0=75, because when the actual population was used, no economically reasonable internal rate of return existed.
*******************************************************************
Figure 8. Summary of Interage Reallocations in Various Contexts
Note: The figure plots estimated average ages from the data used in Figures 3 to 7, where further information on data and methods can be obtained.
********************************************************************
Figure 9. Public Sector Transfers in India (Health, Pensions and Education in 1981)
Note: For details on methods, assumptions and sources, see Lee (1991).
**********************************************************************
Figure10. Familial Transfers in the U.S.
Note: Net familial transfers to children are calculated as described in the note to Figure 5, based on the profiles for consumption and labor earning for ages 0 through 17 (the age interval 15-19 was weighted by .6). Transfers for costs of college were estimated from data in the U.S. Statistical Abstract. Bequest flows were estimated from data discussed in Modigliani (1988). Other interhousehold familial transfers were estimated from data in the Consumer Expenditure Survey, and are surely substantially underestimated. For further details on methods, assumptions and sources, see Lee (1994a).